Esőt a legkisebb gyerekek is ügyesen rajzolnak. Gömbölyded felhőcskével, hegyes kis cseppecskékkel. Ezen gyermekek egy kicsi része később a médiában helyezkedik el (mint sok millióan) és a tévés időjárásjelentésnél ügyesen mutogatja az őszi eső hegyes kis cseppjeit a térképen.

A cseppek (sunyi, de megbocsátható módon) mélyen hallgatnak. Ha benézünk az aktájukba, akkor azonban láthatjuk, hogy az igazolványképpel gond van. Az esőcseppek nem is így néznek ki!
A vízcseppek a legjobb esetben szabadeséssel közelítik meg a szélvédőket, esernyőket és a növényeket. Rosszabb esetben a szél ezt megzavarja. Esés közben (ha szél nincs) csak a gravitáció és a légellenállás hat rájuk. Alakjuk ezért közelít egy gömbhöz. A hegyes cseppalakkal akkor találkozunk, ha a súly is jelen van, azaz a csepp valahol lóg. Például, ha a csöpög a csap. Az esőcseppek alakja akkor lenne ilyen hegyes, ha mondjuk kicsike manócskák tartanák őket esés közben a pici ujjacskáikkal. Ez viszonylag ritkán történik a természetben.
Az esőcseppek alakjával kapcsolatos problémát bárki saját maga is átgondolhatja egy kerekded, vízzel töltött lufi segítségével.

 A képen jól látható a rajzokból is ismert cseppalak (és a kolléganőm keze). Itt fellép a súly, azaz a lufiban levő víz húzza a kolléganőm kezét. Ő ennek ellenáll, tartja a lufit és emiatt kialakul ez az alak.
Ha a lufit leejtjük, akkor esés közben ez az alak eltűnik és a gömbhöz hasonlító formát látunk. (Ha nagyon figyelünk.) (Szabad)esés közben súlytalanság van. Itt látható egy rövidke videó egy vízzel töltött lufi eséséről. A filmecskéből kivágott képen látszik, hogy a hegyes cseppalak az eső esetében téves. Nem akarom a véradásszervezőket bántani, de az ő plakátjaikkal is vannak gondok.

A legfigyelmesebb olvasóknak talán feltűnt, hogy a lufis képek mellett hirtelen egy kis mécses képe is felbukkant. Nos, ha már így kitudódott...
A gyertyaláng felfelé hegyesedő alakja a felhajtóerő miatt van. Ha a gyertyát (mécsest) elejtenénk, akkor esés közben (súly hiányában) felhajtóerő sem hatna és akkor gömb alakú lángot látnánk.

Ez a helyzet.

Köszönöm kollégáimnak a felvételhez nyújtott cseppnyi segítséget.

Felnőtteket kértem arra, hogy rajzoljanak atomokat és molekulákat. Nem azért tettem, mert kíváncsi voltam, hogy okosabbak-e mint egy ötes. Mert amúgy okosabbak voltak. Ráadásul tudták, hogy nem igazán van jó megoldás.
Bocsássuk előre: a kémiatanárok csak azért rajzolnak a táblára ilyesmit, mert modellekkel dolgoznak vagy pedig leplezik az igazságot.

Nézzük meg, milyen atomképek voltak a rajzolók fejében.


Ez az atom nemzetközileg ismert jele. Ez az atom Bohr-Sommerfeld-féle modelljének az ábrázolása. Ebben az atommag körül csak bizonyos ellipszis alakú pályákon keringenek az elektronok. Ez az atom utolsó, jól rajzolható modellje, mely a XX. sz. 20-as éveiben meg is dőlt.



Itt a szerző ugyancsak a Bohr-féle modellre utalhatott, de túl nagynak mutatja az atommagot, mely a valóságban tízezerszer kisebb mint maga az atom. Például ezért is bátor dolog atomot rajzolni. De ahogyan a föniciaiak is mondták: atomot pedig rajzolni kell. (Nem is mondták.)




Ez a piros rajz valószínűleg az atommagban levő protonok és neutronok tumultusát szeretné érzékeltetni atomrajz helyett.
Ha mégis atom lenne, akkor a Thomson-féle mazsolás puding juthat eszünkbe. Ebben a mazsolák a negatív töltésű elektronok, a puding egy pozitív töltésű massza. Ezt a kedves modellt 1909 körül Rutherford kísérlete a történeti érdekességek közé tette.



Nem cicózott a szerző. Tisztázta, hogy az atommag pozitív, a körülötte levő rész pedig negatív. A méretarányok tekintetében jobb lenne a mákszem a focipálya közepén hasonlatával élni.



Itt a XX. század első évtizede köszön nekünk. (Helló.) A szerző itt alighanem a Rutherford-kísérlet eredményére, az atom bolygómodelljére utalt. Az elektronok úgy keringenek az atommag körül, mint a bolygók a Nap körül. Csodaszép modell, de már születésekor kiderült, hogy hibás.



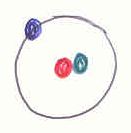
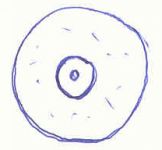Ez a rajz egy sütire emlékeztet (madártávlat). Nem tudom, hogy a középső pötty mire utalhat. Lehetne egy proton az atommagban, de akkor az elektronfelhőben levő vonalkák 1 darab elektront jelölnek, amint a kvantummechanika törvényei szerint nem látszik, helyét csak sejtjük. Az elektronfelhőt éppen  ezért nehéz lerajzolni. Az is igaz, hogy ez esetben a proton sem kis bogyócska, ő is kicsit "szétkenődik".



A legközelebb mai elképzeléseinkhez talán ez a rajz áll. Kérdés, hogy miként tudjuk magunkban elintézni, hogy a valósághoz ez áll a legközelebb, miközben a gerjesztést a Bohr-modellel szoktuk értelmezni, a héjak tanulásakor a diákok pedig olyasmit látnak a tankönyvükben, mint a bolygómodell.




Sokszor fordul elő velünk, hogy a memóriánkba égett tankönyvi ábrák eltakarják azt a képet, amely a valóságról kialakulhatott volna bennünk pl. az atomokról.
Ez a helyzet.

Arkhimédész törvénye olyan mint egy film, amit mindenki látott, mégsem mindenki tudja, hogy miről szól. A főszereplő még rémlik és a reklámszöveg is, aztán kakukk.
A kisangyalommal giccsesített nótácska számomra igazi idegborzoló horrormúvi. A "minden vízbe mártott test, a súlyából annyit veszt, amennyi az általa kiszorított víz súlya" sorok eléggé helybenhagyják a fizika egyik szép törvényét.

Nézzük meg, hogy miért!
Először is a törvény messze túlmutat a vizen, mivel más folyadékban is érvényes, például higanyban is. Sőt, legyünk erősek: gázokban is érvényesül. Jut eszembe, mi nehezebb? 1 kg toll vagy 1 kg vas?
Másodszor a testek mártogatása leginkább a pörköltszaft szakterülete. Legyen inkább (el)merülés.
Harmadszor a súlyvesztés a rím miatt került át a fitnessguruk szótárából. Nem hibás, de pontatlan és fátylat borít a lényegre.

Az ókor egyik legérdekesebb természettudósa jó érzékkel ötvözte a matematikát azzal, amit ma fizikának nevezünk. Nem láthattuk valóságshow keretén belül, ahogy a fürdőben meztelenül rájött a később általa híressé vált törvényszerűségre. Talán igaz a legenda, talán nem. De szívesen meséljük, hogy meztelenül, kiáltozva rohant Szirakúza utcáin és kiabálta: Heuréka! (Megtaláltam!) Száva István A szirakúzai óriás című könyve kellemes olvasmány, ajánlom. Jut eszembe, mi nehezebb? 1 kg toll vagy 1 kg vas?

A mártogatós súlyvesztésnél azonban itt többről van szó, kisméretű angyalom! Minden folyadékba vagy gázba merülő testre felhajtóerő hat, melynek nagysága egyenlő a kiszorított folyadék vagy gáz súlyával.
A felhajtóerő függ a test térfogatától, azaz a dinnye jobb helyzetben van a ribizlinél. Ez az erő a sűrűségtől is függ, de csupán a közeg sűrűségétől. Ez azt jelenti, hogy a dinnyére és egy ugyanakkora ágyúgolyóra ugyanakkora felhajtóerő hat mondjuk vízben.

Jut eszembe, mi nehezebb? 1 kg toll vagy 1 kg vas? Ebben a kérdésen az ovisok is szakértők és a felnőttek is nagy lelkesedéssel villognak vele gyermektársaságban. A válasszal azonban sokan úgy vannak, mint azon emberi társaink, akik számára Einstein csak egy lobogó, fehér hajú, nyelvet nyújtogató bácsi.

Rövid válasz: a vas.
Rossz válasz (kisgyerekeknél megengedett): hát egyforma, te pupák!
Hosszú válasz: hol mérjük? Levegőben esetleg vagy ravaszul vákuumban?

A tömege a vasnak és a tollnak is 1 kg. Ám a toll sokkal nagyobb térfogatot foglal el (szorít ki a levegőből), ezért rá nagyobb felhajtóerő hat a levegőben, mint a vasra, mely kisebb térfogatú. Ha levegőben mérünk, akkor a mérleg tollas serpenyője kissé magasabban lesz. Ha nincs közeg, nem merül a két test semmibe, azaz vákuumban mérünk, akkor egyenlőség lesz.

Ez a helyzet.